Universe Viewer

Universe Viewer est un logiciel interactif de visualisation et de traitement géodésique d'objets astronomiques à grand décalage spectral (redshift).

Il permet de produire une cartographie conforme de structures cosmologiques, plus particulièrement des quasars, en prenant en compte la courbure de l'univers.
Reposant sur des concepts d'astronomie et de relativité générale, il est conçu pour être un outil de travail pour la recherche en cosmologie, facilitant l'identification de structures à grande échelle dans l'espace comobile ou dans un espace de référence.

Ce projet repose sur les concepts développés dans la publication Framework for cosmography at high redshift, par R. Triay, L. Spinelli, R. Lafaye.

C'est un logiciel libre, et son code source est disponible sur sa page GitHub.

Cette version web du logiciel a été portée à partir de la version Java (qui n'est plus maintenue aujourd'hui), avec l'aide de l'intelligence artificielle pour accélérer les séquences fastidieuses de conversion de code de Java / Swing / JOGL vers JavaScript / Vue.js / Vuetify / Three.js.

Je remercie particulièrement le Pr. Roland Triay pour son aide lors de la conception de la version Java du logiciel, réalisée dans le cadre de ma formation en Master lors d'un travail d'étude et de recherche (TER), réalisé en binôme avec Julie Fontaine, en 2008.

Des versions encore plus anciennes d'un logiciel similaire ont existé, en Fortran et en C, basées sur la même publication de recherche, mais elles souffraient de problèmes de portabilité.

Projection de la carte des objets

Le Framework for cosmography at high redshift présente un cadre de travail pour projeter les objets étudiés sur un plan, en fonction des paramètres cosmologiques choisies et du point de vue.

Ces objets sont définis par trois caractéristiques principales:

• l'ascension droite, le premier terme associé au système de coordonnées équatoriales, c'est l'azimut, l'équivalent sur la sphère céleste de la longitude terrestre,
• la déclinaison, le second terme, qui mesure l'angle d'un objet de l'équateur céleste, c'est l'élévation, l'équivalent de la latitude terrestre,
• et le décalage vers le rouge du spectre de l'objet, qui est un effet relativiste permettant d’estimer sa distance par rapport à l'observateur.

C'est donc à partir de ces données que sont représentés les objets à l'écran. Dans un premier temps, la projection sur l'espace de référence a été développée pour le cas d'une courbure positive de l'univers, puis ce travail a été généralisé à la courbure négative.
Les calculs ont finalement été étendus pour la représentation en espace comobile, qui fait abstraction de l'expansion de l'univers.

Calcul de la distance comobile

La distance comobile (sans unité) est notée $\tau$, elle dépend du décalage vers le rouge z de l'objet concerné et on la calcule de la manière suivante:

$$\tau (z)={\int }_{(1+z{)}^{-1}}^1\frac{da}{\sqrt{P(a)}}$$

avec:

$$P(a)={\lambda }_0{a}^4-{\kappa }_0{a}^2+{\mathrm{\Omega }}_{0}a+{\alpha }_0$$$$P(1)=1$$

où ${\lambda }_0$, ${\kappa }_0$, ${\alpha }_0$, ${\mathrm{\Omega }}_0$ sont les paramètres cosmologiques:

• ${\lambda }_0$, une constante cosmologique représentant l'énergie du vide,
• ${\kappa }_0$, le paramètre de courbure, qui définit la géométrie globale de l'univers,
• ${\alpha }_0$, qui quantifie la présence de photons du fond diffus cosmologique comme source de gravitation,
• ${\mathrm{\Omega }}_0$, le paramètre de densité de matière gravitationnelle,

et a représente le facteur d'échelle cosmologique. Pour un objet observé avec un décalage vers le rouge z, il vaut:

$$a(t)=\frac{1}{1+z}$$

Ce facteur d'échelle décrit l'état d'expansion de l'Univers au moment où la lumière a été émise. Aujourd'hui, on a $a_0=1$.

Normalisation de la distance comobile en géométrie courbe

Lorsque l'espace comobile n'est pas plat (${\kappa }_0\ne 0$), on introduit la distance angulaire:

$$\hat{\tau }=\tau \sqrt{|{\kappa }_0|}\text{avec}{\kappa }_0\ne 0$$

Cette variable apparaît naturellement dans la métrique spatiale à courbure non nulle:

$$\{\begin{array}{ll}R=\frac{\sin (\hat{\tau })}{\sqrt{{\kappa }_0}}& {\kappa }_0>0\\ R=\frac{\sinh (\hat{\tau })}{\sqrt{-{\kappa }_0}}& {\kappa }_0<0\end{array}$$

Dans le cas particulier de l'espace plat (${\kappa }_0=0$):

$$R=\tau$$

R est utilisé pour placer les points dans la géométrie courbe.

Calcul de la projection sur le plan d'observation

Chaque objet cosmologique est représenté par un vecteur 4D dans l'espace-temps homogène du modèle:

$$\overrightarrow{X}=(x,y,z,t)$$

Les trois premières coordonnées (x, y, z) représentent la position spatiale de l'objet dans l'espace 3D d'immersion correspondant à la géométrie choisie (sphérique si ${\kappa }_0$ > 0, hyperbolique si ${\kappa }_0$ < 0, ou plate si ${\kappa }_0$ = 0).
La quatrième coordonnée t représente la composante temporelle conforme (associée à la distance comobile $\tau$) dans l'espace-temps homogène.

Les coordonnées x, y et z sont calculées de la façon suivante:

$$x=R\cos (De{c}_{obj})\cos (R{A}_{obj})$$$$y=R\cos (De{c}_{obj})\sin (R{A}_{obj})$$$$z=R\sin (De{c}_{obj})$$

où $R{A}_{obj}$ et $De{c}_{obj}$ sont l'ascension droite et la déclinaison de l'objet.

Dans l'espace de référence, $t=\tau$, et dans l'espace comobile:

$$t=\tau \sqrt{|{\kappa }_0|}$$

L'affichage 2D nécessite de projeter ce vecteur 4D sur un plan image, qui représente le plan du ciel selon le point de vue.

Construction de la base locale d'observation

L'utilisateur définit son orientation dans l'univers à l'aide de trois angles:

• RA1, l'ascension droite (azimut),
• Dec1, la déclinaison (élévation),
• Beta, la rotation autour de l'axe de visée (roulis).

À partir de ces angles, on construit trois vecteurs orthonormés dans l'espace 3D euclidien:

• $\overrightarrow{P_1}$: direction du regard (centre de la projection),
• $\overrightarrow{P_2}$: direction horizontale locale,
• $\overrightarrow{P_3}$: direction verticale locale.

Ces trois vecteurs forment une base orthonormée spatiale.
Dans l'espace-temps 4D du modèle, cette base devient:

$${\overrightarrow{E}}_1=\left(\begin{array}{c}\overrightarrow{P_1}\\ 0\end{array}\right)\text{,}{\overrightarrow{E}}_2=\left(\begin{array}{c}\overrightarrow{P_2}\\ 0\end{array}\right)\text{,}{\overrightarrow{E}}_3=\left(\begin{array}{c}\overrightarrow{P_3}\\ 0\end{array}\right)$$

Le quatrième vecteur de base est défini comme:

$${\overrightarrow{E}}_0=\left(\begin{array}{c}\overrightarrow{0}\\ s\end{array}\right)$$

où:

$$s=\{\begin{array}{ll}1& \text{dans l’espace de référence}\\ \sqrt{|{\kappa }_0|}& \text{dans l’espace comobile}\end{array}$$

Ce vecteur encode la composante temporelle du repère. Sa normalisation dépend de l'espace choisi (référence ou comobile), car cela garantit que les projections respectent la métrique du modèle.

Projection sur le plan image

Pour un objet dont le vecteur 4D est $\overrightarrow{X}$, ses coordonnées projetées sur le plan 2D sont:

$$x_{\text{proj}}=\overrightarrow{X}\cdot {\overrightarrow{E}}_1=X_x{E}_{1x}+X_y{E}_{1y}+X_z{E}_{1z}+X_t{E}_{1t}$$$$y_{\text{proj}}=\overrightarrow{X}\cdot {\overrightarrow{E}}_2=X_x{E}_{2x}+X_y{E}_{2y}+X_z{E}_{2z}+X_t{E}_{2t}$$

Exemples de projections

Hewitt & Burbidge QSO Catalog

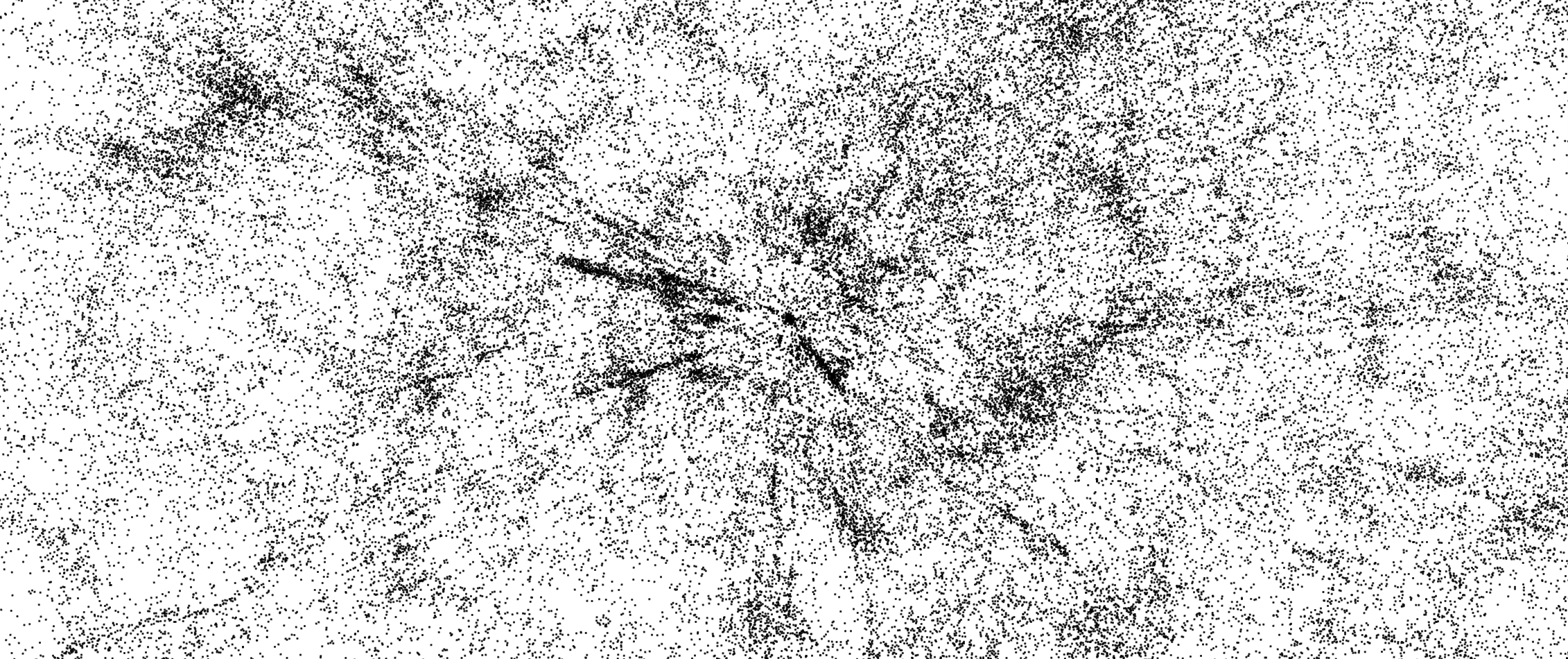
Voici quelques projections obtenues sur le catalogue de quasars Hewitt & Burbidge, composé de 7 236 objets.

La zone bleue représente l'univers visible, la ligne grise qui l'entoure l'horizon cosmologique.

La zone blanche représente l'univers visible, la ligne noire qui l'entoure l'horizon cosmologique.

Vue de face, courbure positive

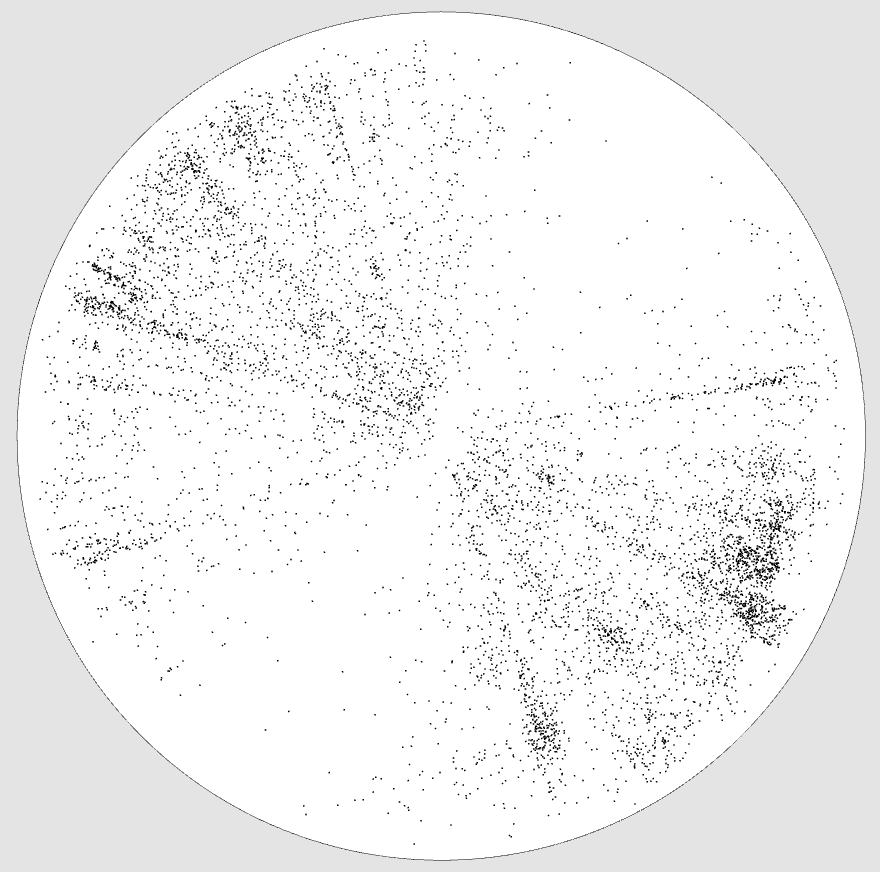Notre galaxie se trouve au centre.

Vue de côté, courbure positive

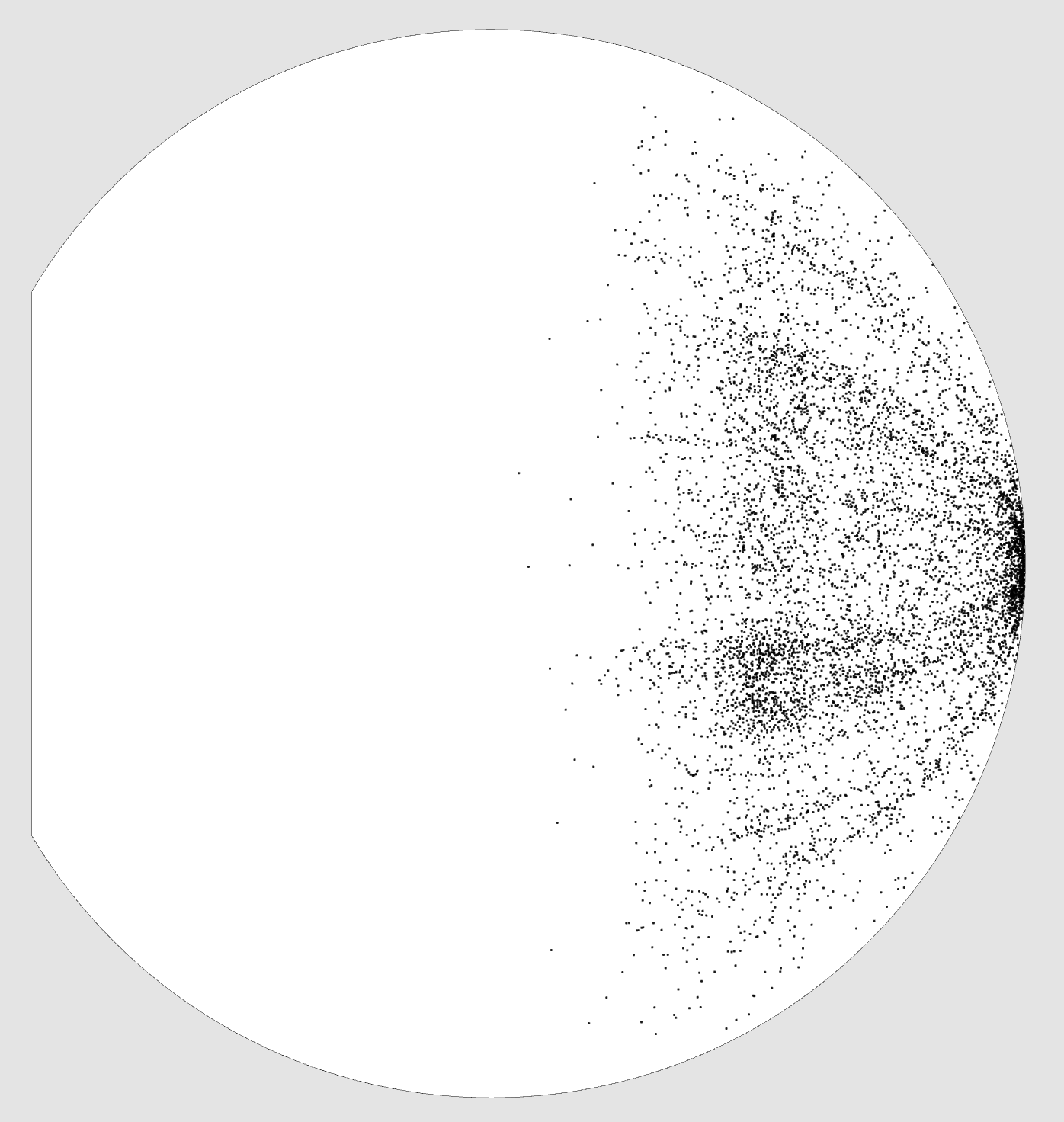Notre galaxie se trouve tout à droite.

Vue de côté, courbure négative

Notre galaxie se trouve tout à gauche.

Vue du ciel

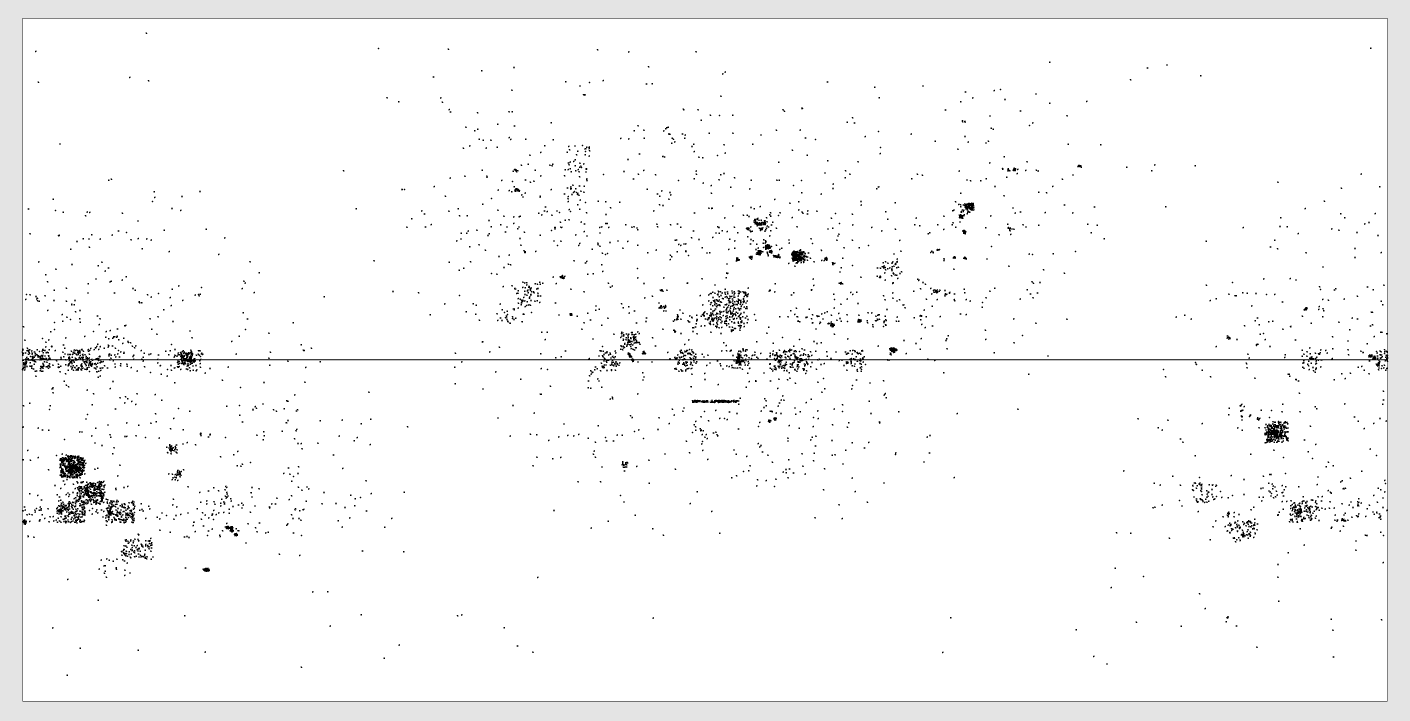Nous voyons ici ce que les radiotélescopes ont observé depuis la terre.

Sélection d'objets

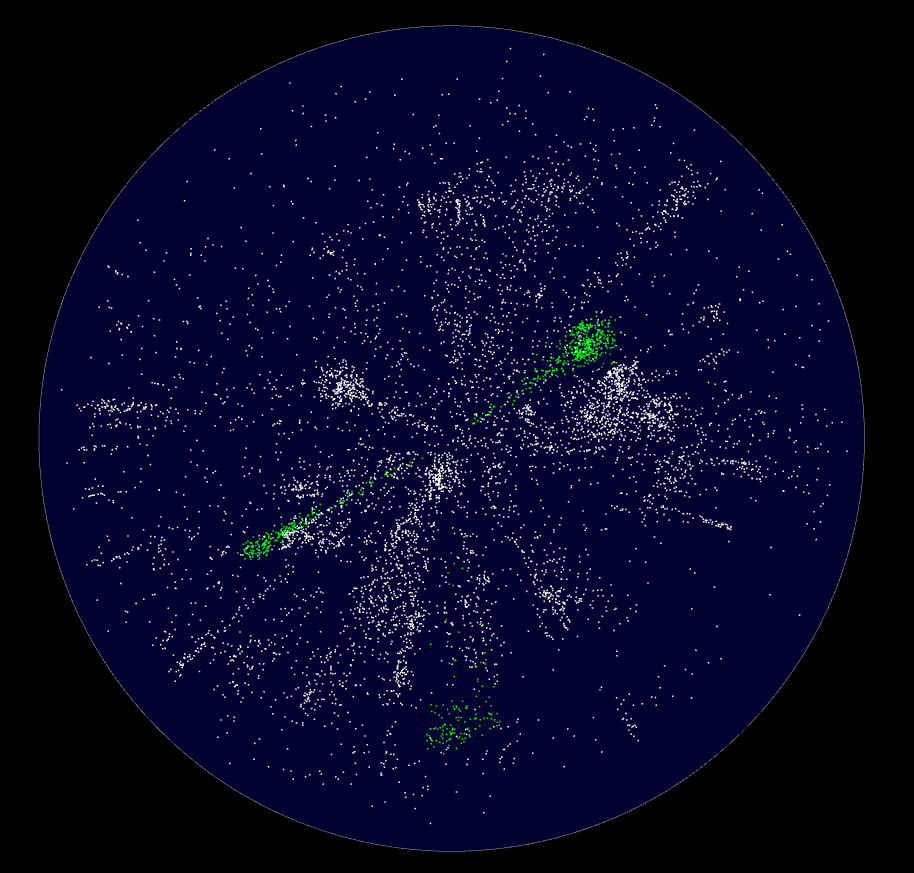
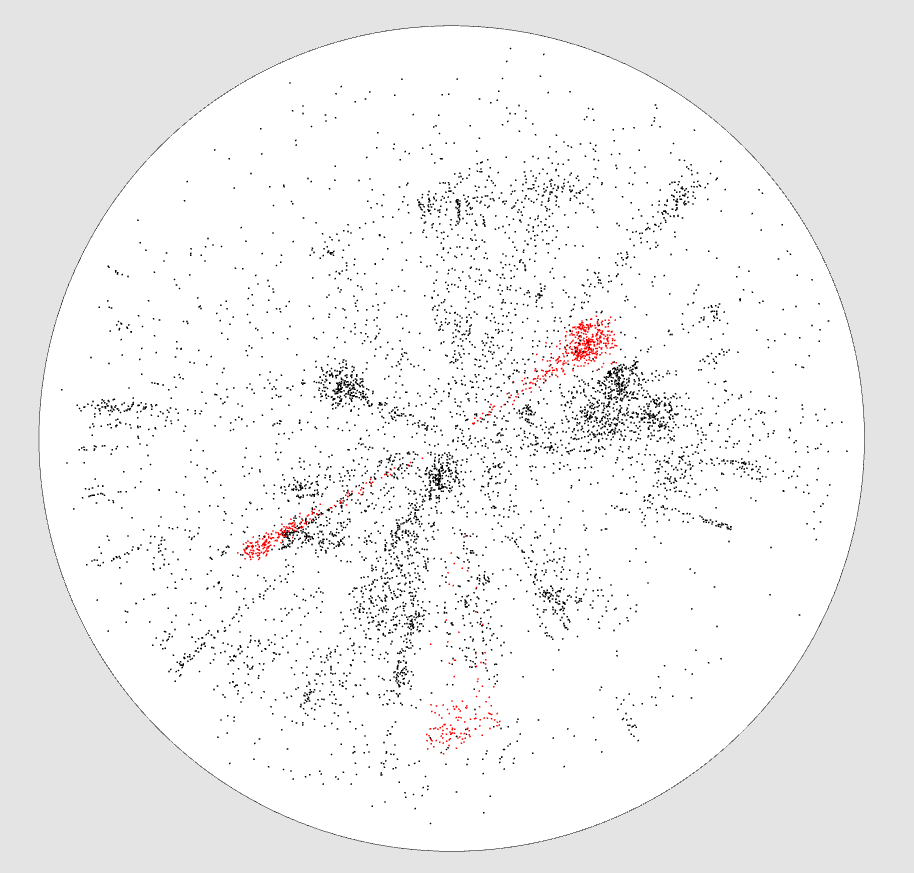On peut sélectionner des objets avec une sélection additive ou d'intersection, qui permet de sélectionner précisément des zones.

Les objets sélectionnés apparaîssent en vert.

Les objets sélectionnés apparaîssent en rouge.

6dF Galaxy Survey

Le catalogue 6dF Galaxy Survey est composé de 124 646 objets.

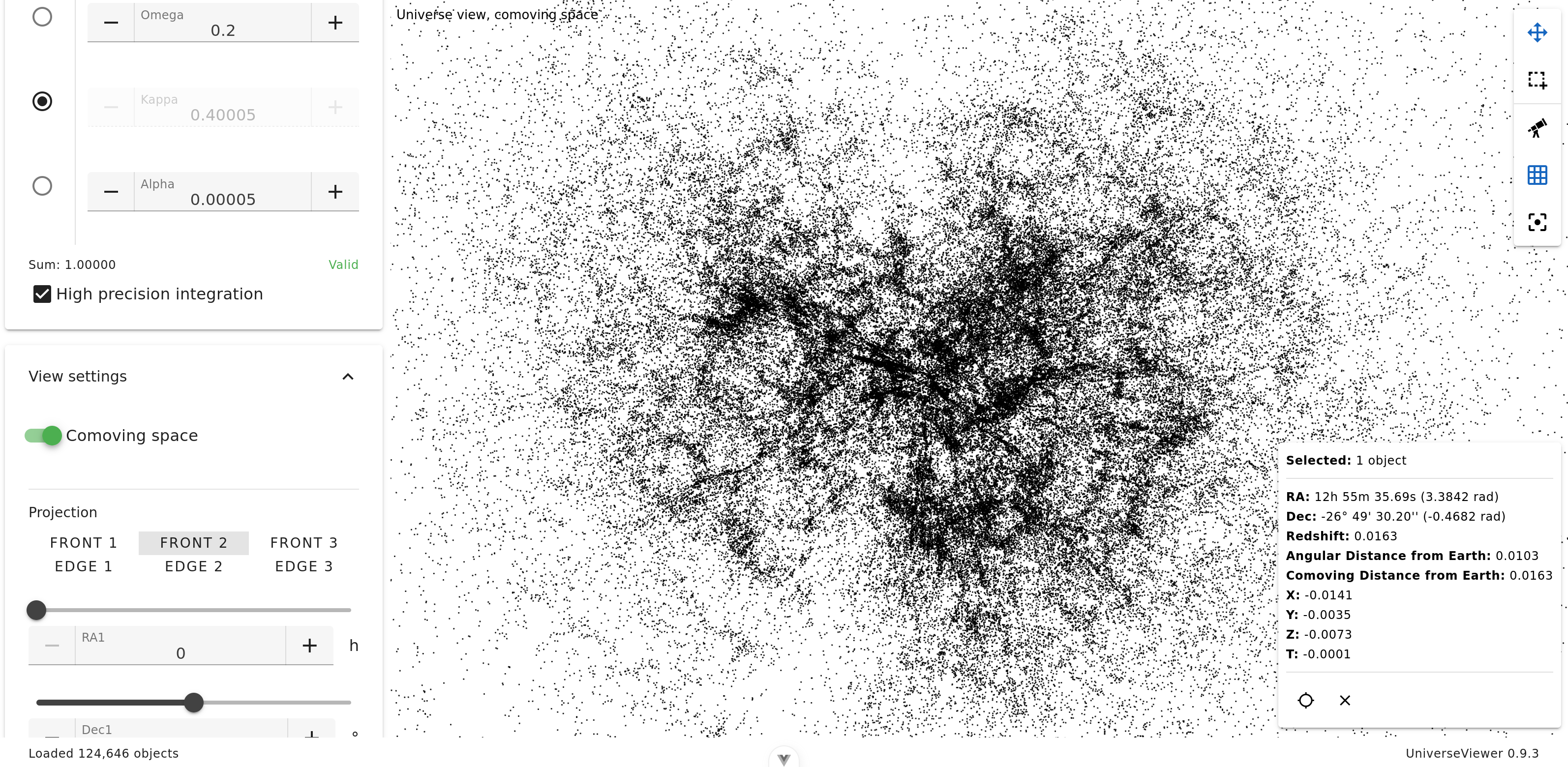
Zoom

Ici nous sommes en vue de face n°2, et la projection est zoomée avec notre galaxie approximativement en son centre.

Quasars (13th Ed.) (Veron-Cetty+)

Ce catalogue est composé de 133 335 objets.

Coloration en dégradé du redshift

Pour mieux apprécier le redshift des objets affichés, il est possible de leur appliquer une coloration.

Les objets les plus proches de notre galaxie sont en bleu, les plus éloignés en rouge.

Les objets les plus proches de notre galaxie sont en vert, les plus éloignés en bleu.

Calcul de la distance entre deux objets

Soient $x_1$ et $x_2$ les directions dans le ciel de deux objets, on peut calculer l'angle apparent entre eux:

$$\cos {\theta }_{12}=⟨x_1,x_2{⟩}_3$$

qui se traduit par:

$$\begin{array}{r}\cos {\theta }_{12}=\cos (R{A}_{obj1}-R{A}_{obj2})\cos (De{c}_{obj1})\cos (De{c}_{obj2})\\ +\sin (De{c}_{obj1})\sin (De{c}_{obj2})\end{array}$$

Pour calculer la distance géodésique entre ces objets dans un espace de courbure non nulle, nous avons deux cas à considérer:

pour $k_0>0$ (sphérique),

$$\begin{array}{l}\cos {\hat{\tau }}_{12}=\cos {\theta }_{12}\sin {\hat{\tau }}_1\sin {\hat{\tau }}_2+\cos {\hat{\tau }}_1\cos {\hat{\tau }}_2\\ {\hat{\tau }}_{12}=\arccos (\cos {\hat{\tau }}_{12}),\end{array}$$

pour $k_0<0$ (hyperbolique),

$$\begin{array}{l}\cosh {\hat{\tau }}_{12}=\cosh {\hat{\tau }}_1\cosh {\hat{\tau }}_2-\cos {\theta }_{12}\sinh {\hat{\tau }}_1\sinh {\hat{\tau }}_2\\ {\hat{\tau }}_{12}=\mathrm{arccosh}(\cosh {\hat{\tau }}_{12}),\end{array}$$

où ${\hat{\tau }}_1$ et ${\hat{\tau }}_2$ sont les distances angulaires des objets par rapport à la Terre.

Nous pouvons obtenir la distance comobile sans unité avec:

$${\tau }_{12}=\frac{{\hat{\tau }}_{12}}{\sqrt{|k_0|}}$$

Pour le cas particulier $k_0=0$ (espace plat), on applique la loi des cosinus en géométrie euclidienne:

$${\tau }_{12}=\sqrt{{\tau }_1^2+{\tau }_2^2-2{\tau }_1{\tau }_2\cos {\theta }_{12}},$$

Il est alors possible d'exprimer la distance en Mpc:

$$r={\tau }_{12}\frac{c}{H_0}$$

où $c$ est la vitesse de la lumière en km/s, soit 299792.458 km/s, et $H_0$ la constante de Hubble.

Implémentation

Voici quelques choix techniques concernant l'implémentation.

Calcul d'intégrales

Deux façons de calculer les intégrales ont été implémentées:

• la méthode de Romberg, rapide au détriment de la précision,
• la méthode des trapèzes, plus lente, mais plus précise.

Parallélisation des traitements

Par défaut, dans un navigateur web le JavaScript s'exécute dans la boucle principale, qui s'occupe également du code de rendu de la page. Non seulement cette boucle n'utilise qu'un seul cœur du processeur, mais les calculs intensifs figent l'interface utilisateur.

Nous avons une grande quantité d'objets pour lesquels nous calculons la projection en fonction des paramètres cosmologiques. Cet ensemble d'objets peut très facilement être découpé en plusieurs morceaux pour que les traitements soient effectués sur plusieurs cœurs en même temps.

Cette parallélisation dans Universe Viewer utilise les web workers, qui nous permettent de découper le travail en fonction du nombre de cœurs disponibles sur le processeur.
Ce processus est réalisé dans les fichiers suivants:

• workerPool.js, qui gère la pool de workers, leur cycle de vie et leur exécution pour le calcul des projections,
• projectionWorker.js, le code des tâches des workers, qui réalise les traitements sur un sous-ensemble des objets,
• projection.js, les fonctions de calcul des projections.

Si le nombre d'objets à traiter se trouve en-dessous d'un certain seuil, le calcul n'est pas parallélisé car le surcoût engendré par gestion des processus serait contre performant.

Pour rendre la parallélisation encore plus pertinente, nous utilisons de la mémoire partagée entre les processus de calcul et le rendu graphique, via un SharedArrayBuffer: nous évitons toute recopie de données dès lors qu'un catalogue a été chargé.

Si SharedArrayBuffer est indisponible, par exemple à cause d'une contrainte de sécurité non respectée, les calculs ne sont pas parallélisés.

Ces optimisations rendent UniverseViewer capable de gérer des catalogues de millions d'objets, comme AGN/QSO Value-Added Catalog for DESI DR1, ou Million Quasars Catalog, Version 8.

---

Site officiel
Page GitHub
Framework for cosmography at high redshift - R. Triay, L. Spinelli, R. Lafaye (1996), version HTML, et version PDF textuelle
Calcul d'intégrales avec la méthode de Romberg
Calcul d'intégrales avec la méthode des trapèzes
Ancienne version Java